Покерная математика: связь между сложным EV и простыми шансами банка.

Привет, Cardmates!

Хотел сегодня подготовить пост с раздачами, но в процессе обратил внимание на расхождение, которое показываем мне Hand2Note между выигрышем от раздачи и EV. Начал разбираться с понятие EV, давно следовало сделать.

Как и в предыдушем посте про математику, для тех кому скучно и хочется сразу десерта, можно пролистать пост до раздела Выводы (там где Старк закатывает глаза), а если заинтересуетесь, откуда эти цифры, можно вернуться к описанию.

Пожалуйста не пожалейте своей оценки, даже если поленитесь все прочитать. Я очень старался)))

ВНИМАНИЕ ОПАСНОСТЬ: Дальше очень много букв!!!

EV (Expected Value) - это математическое ожидание ваших действия при розыгрыше. Т.е. какой результат (выигрышь/проигрышь) в суммарном выражении ожидать, если вы будете действовать аналогичным образом в большом количестве рук. На примере поясню позже.

В книгах по покерной математике приводятся методики расчета, которые должны облегчить покеристу принятие решение прямо за игровым столом. Для этого используются понятия: шансы банка и шансы на победу. Эти шансы можно рассчитывать как в виде шансов против: 1:4, 1:2, 2:3 и т.д., так и в виде процентов: 20%, 33%, 40%

Если мы считаем шансы против, то шансы банка должны быть выше чем наши шансы на победу, чтобы наше действие было прибыльным.

Если мы считаем шансы ввиде процентов, то шансы банка должны быть ниже, чем наши шансы на победу, чтобы наше действие было прибыльным.

Не очень понятно поясню на примере.

Пример:

Терн: A♦T♦8♠   2♥

Наши карты: 6♦5♦

У оппоннента, например (тут это не так важно): A♣K♠

Нам необходимо собрать flush, чтобы выиграть. Следовательно у нас 9 аутов. Наши шансы на победу составляют около 20%. Нас устроят 9 карт из оставшихся 44.

Предположим в банке 500 фишек. Оппонент пошел all-in ставкой 500. Следовательно в банке 1000. И нам необходимо ответить ставкой 500.

Давайте сделаем несколько расчетов.

EV

В самом простом случае EV считается, как сумма произведений:

1. Шансов на победу на сумму фишек, которые мы можем в результате выиграть

2. Шансов на проигрыш на сумму фишек, которые мы должны поставить на данный момент в банк.

EV = 20% * 1000 - 80% * 500 = -200

Т.е. результат нашего call'а при сыгрывании большого количества аналогичных раздач, будет минусовым.

-200 означает, что в среднем на одну раздачу мы проиграем 200 фишек.

Т.е. 1000 - 500 - 500 - 500 - 500 = -1000 мы сыграли 5 раздач и проиграли 1000 фишек, в среднем 200 фишек за раздачу.

Это очень важно:

EV показывает наш результат на одну раздачу, а не за серию раздач. -200 это не суммарный результат 5 раздач, а всего лишь одной.

Шансы против

Необходимо посчитать шансы банка и шансы на победу.

Шансы банка: (Pot + Bet) : Call, т.е. (500 + 500) : 500 = 2 : 1 - шансы банка составляют 2 к 1, т.е. мы ставим одну ставку, чтобы выиграть 2

Шансы на победу: Оставшиеся карты в колоде : ауты на победу, т.е. 44 : 9 или 5 : 1

Имеем, что шансы против банка меньше, чем шансы против нашей победы. Следовательно в среднем при большом сыгрывании рук в аналогичной ситуации мы будем в минусе. Аналогичный вывод, что и для EV.

Шансы в процентах

Так же необходимо посчитать шансы банка и шансы на победу.

Шансы банка: Call / (Por + Bet + Call), т.е. 500/(500 + 500 + 500) = 33% - шансы банка составляют 33%.

Шансы на победу: вероятность получить наш аут составляют 20%.

Имеем, что шансы банка выше, чем наши шансы на победу. Следовательно в среднем при большом сыгрывании рук в аналогичной ситуации мы будем в минусе. Аналогичные вывод, что и для предыдущих двух расчетов.

Выводы:

Мне пришла в голову идея, проверить связь между EV и шансами, которые можно легко расчитывать прямо во время игры. Я составил небольшую табличку в Excel. Понятно, что в зависимости от первоначальной суммы уже имеющейся в банке при прочих равных, наше действие будет либо выгодным, либо нет. Наше EV будет либо плюсовым, либо минусовым.

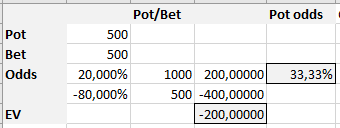
Вот таблица для выше изложенного случая:

Шансы банка выше чем, наши шансы на победу.

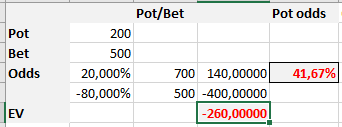
А что если, изначально в банке будет меньше фишек, значит наш ожидаемый EV будет иметь еще больший минус, а шансы банка будут еще больше.

Значит возможно ситуация, когда размер изначального банка, настолько велик, что мы можем смело отвечать call'ом и при этом играть в этой ситуации в ноль. А при банке еще большем, мы будет уже в плюсе.

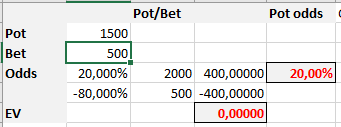
В последней таблице мы видим, что если наш соперник сделает ставку равную 33% от банка, наш EV становится равным 0, а шансы банка сравнялись с нашими шансами на победу. Т.е. в среднем в при сыгрывании большого количества рук, мы будет не в плюсе и не в минусе.

Таким образом, я проверил, что использование простых шансов банка, действительно работает так же эффективно, как и расчет сложного EV, который зачастую просчитать без спецаильных программ просто невозможно (ведь нам необходимо просчитать наш EV на каждой улице).